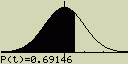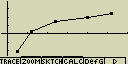|
|
http://archaikum.cz/casio/kalkulacky/algebra/manual/mod02_stat.php |
| [ Archaikum.cz > CASIO > grafické kalkulačky > ALGEBRA FX 2.0 / PLUS > manuál > Manuál k ALGEBŘE FX 2.0 - mód STAT ] |
Statistika (mód STAT)


- Možnosti seznamu (Listu)
- 3-1 Vkládání a úpravy seznamu
- 3-2 Zpracování dat v seznamu
- 3-3 Použití seznamu (Listu) ve výpočtu
- 3-4 Přepínání mezi soubory seznamů
- Statistické výpočty a grafy
Možnosti seznamu (Listu)
V kalkulačce lze vyhradit paměťový prostor k uložení vlastní řady čísel.
Tento prostor je rozdělen do souborů kterých může být až šest. V každém
jednotlivém souboru jsou tzv. seznamy (Listy) kterých každý soubor obsahuje
dvacet. Každý seznam (List) obsahuje maximálně 255 řádků
Seznamy (Listy) můžeš použít v aritmetických a statistických výpočtech
nebo hodnoty v nich uložené použít pro grafický výstup

3-1 Vkládání a úpravy seznamu
Vkládání hodnot buňka po buňce
Na displeji je zobrazen vždy jeden soubor ve kterém sloupce představují
jednotlivé seznamy (Listy). Čísla v řádcích odpovídají pozici v seznamu
(Listu)

pomocí kurzorových kláves se přesuň na požadovaný seznam (List) a pozici
v něm. Pokud se dostaneš kurzorem mimo zobrazenou oblast, výřez z tabulky se
automaticky posune
- Zadej hodnotu a stiskni [EXE]
[3][EXE]
Kurzor se automaticky posune na pozici o řádek níž - Do další buňky zadej hodnotu 4 a do další vlož součet 2+3
[4][EXE]
[2][+][3][EXE]
- Do buňky lze vložit výsledek výrazu nebo komplexní číslo
- Jeden seznam (List) může obsahovat až 255 záznamů (řádků či buňek)
Vkládání hodnot do více buněk současně
- Pomocí kurzorových kláves se přesuň na další seznam (List)

- Stiskni [SHIFT][×]({) a zadej požadované hodnoty oddělené čárkou
",". Po vložení posledního údaje stiskni [SHIFT][
 ](})
](})
- Stiskni [EXE] a zadané hodnoty se vloží do seznamu (Listu)
Obsah buňky lze vložit zapsáním matematického výrazu který obsahuje odkazy na jiné buňky z daného souboru (tj. z různých seznamů (Listů))
Do seznamu (Listu) 3 zadej součet buněk ze seznamu (Listu) 1 a 2
- Kurzorovými šipkami označ seznam (List) do kterého chceš vložit výsledek
- Napiš [OPTN][F1](LIST)[1](List)[1][+]
[OPTN][F1](LIST)[1](List)[2]

[EXE]
- Uzavírací závorka } a ) na konci výrazu je nepovinný údaj, nemusí se psát
- [OPTN][F1](LIST)[1](List) lze nahradit použitím [SHIFT][1](List)
- Uvědom si, že čárka při zápisu do více buněk odděluje jednotlivé
hodnoty a nelze ji tudíž použít před uzavřením závorky
správně: {46,47,58,98}
špatně: {46,47,58,98,}
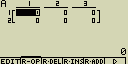
Úprava hodnot v seznamu (Listu)
- Pomocí kurzorových kláves se přesuň na buňku, jejíž hodnotu chceš změnit
- Pro úpravu obsahu stiskni [F6](
 )[F2](EDIT)
a obsah buňky se zobrazí v řádku pod tabulkou
)[F2](EDIT)
a obsah buňky se zobrazí v řádku pod tabulkou
Odstranění buňky ze seznamu (Listu)
- Pomocí kurzorových kláves se přesuň na buňku kterou chceš odstranit
- Stiskem [F3](DEL) nebo [DEL] buňku odstraníš. Současně se buňky následující
po buňce odstraněné posunou o jednu pozici směrem nahoru
Operace odstranění se týká pouze zvolené buňky v aktuálním seznamu
(Listu) a nemá vliv na buňky v jiných seznamech (sloupcích). Pokud byl obsah
jiné buňky svázán (odkazem ve vzorci) s obsahem odstraněné buňky, může
dojít ke zkreslení přepočítávaných hodnot vlivem změny odkazovaných
pozic
Odstranění všech buněk ze seznamu (Listu)
- Pomocí kurzorových kláves se přesuň na buňku, jejíž hodnotu chceš změnit
- Po stisknutí [F4](DEL.A) se objeví dotaz na potvrzení operace
- Seznam (List) definitivně odstraníš stiskem [EXE] nebo odstranění zrušíš stiskem [ESC]
Vložení nové buňky do seznamu (Listu)
- Pomocí kurzorových kláves se přesuň na místo kam chceš vložit buňku

- Pro vložení nové buňky stiskni [F5](INS)
Obsahem nové buňky bude hodnota 0
Všechny buňky pod buňkou vloženou se posunou o jednu pozici směrem dolů
Vložení buňky se projeví jen v aktuálním seznamu (Listu) a nemá vliv na
buňky v jiných seznamech (sloupcích). Pokud byl obsah jiné buňky svázán
(odkazem ve vzorci) s obsahem buňky ve změněném seznamu (sloupci), může
dojít ke zkreslení přepočítávaných hodnot vlivem změny odkazovaných
pozic
Seřazení hodnot v seznamu (Listu)
Seznam (List) lze seřadit ve vzestupném nebo sestupném pořadí
Seřazení jednoho seznamu (Listu)
1) vzestupné seřazení
- V módu STAT stiskni [F6](
 )[F1](SORT)[1](SortA)
)[F1](SORT)[1](SortA) - Na dotaz na počet seznamů (Listů) zadej hodnotu „1“

- Následně zadej číslo seznamu (Listu) který chceš seřadit
Zadej například [1][EXE]

- Výsledek:
2) sestupné seřazení
Pro sestupné seřazení se použije stejný postup, pouze se místo funkce [1](SortA)
zvolí funkce [2](SortD)
Seřazení více seznamů (Listů)
Můžeš propojit více seznamů (Listů) dohromady tak, že jejich hodnoty (buňky)
budou seřazeny podle jednoho základního seznamu (Listu). Poté bude ve
vzestupném nebo sestupném pořadí seřazen pouze základní seznam (List),
zatímco ostatní seznamy (Listy) budou seřazeny v závislosti na něm (řadí
se celé řádky, ne jednotlivé buńky)
1) vzestupné seřazení
- V módu STAT stiskni [F6](
 )[F1](SORT)[1](SortA)
)[F1](SORT)[1](SortA) - Zadej počet řazených seznamů (Listů)

Seznamy (Listy) budou seřazeny podle jednoho základního seznamu podle něhož se určí řazení a ostatní se podle předešlého přerovnají
Zadej například [2][EXE] - Zadej číslo základního seznamu (Listu), podle něhož se určí seřazení
ostatních seznamů (Listů)
Zadej například [1][EXE]
- Postupně zadávej čísla dalších seznamů (Listů), které chceš seřadit
Zadej například [2][EXE]

- Výsledek:
2) sestupné seřazení
Pro sestupné seřazení se použije stejný postup, pouze se místo funkce [1](SortA)
zvolí funkce [2](SortD)
- Jako počet řazených seznamů (Listů) lze zadat číslo v rozmezí 1 až 6
- Pokud určíš jeden seznam (List) vícekrát (např. jako „Základní
seznam” i „Druhý seznam”) zobrazí se
chybové hlášení

- Stejná chyba nastane i v případě, že seznamy (Listy) určené k seřazení mají rozdílný počet členů (dimenzi)
- Pokud chceš seřadit všechny seznamy (Listy) v souboru, zadej jako parametr „počet seznamů” hodnotu „0”. Potom stačí zadat jen „Základní seznam” podle něhož proběhne seřazení všech seznamů (Listů). I v tomto případě musí mít všechny seznamy (Listy) stejný počet členů (dimenzi)
3-2 Zpracování dat v seznamu
Údaje ze seznamu (Listu) mohou být použity v aritmetických výpočtech nebo
jako součást funkcí
V módech RUN.MAT, STAT, GRPH.TBL,
EQUA a PRGM jsou k
tomuto účelu k dispozici funkce pro zpracování těchto údajů
Přístup k nabídce funkcí pro práci s údaji v seznamu
(Listu)
Následující příklady jsou prováděny v módu RUN.MAT
K nabídce funkcí pro práci se seznamy (Listy) se lze dostat stiskem [OPTN][F1](LIST)
V nabídce jsou tyto funkce:
Ve všech funkcích mohou být vynechány uzavírací závorky na konci výrazu
Zjištění počtu buněk (dimenze) seznamu (Listu)
[OPTN]-[LIST]-[Dim]
[OPTN][F1](LIST)[2](Dim)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[EXE]
Dim List <1...20>
- Počet buněk v seznamu (Listu) udává současně i jeho velikost
Urči počet buněk (dimenzi) seznamu List 1 (36,16,58,46,56)
[AC][OPTN][F1](LIST)[2](Dim)
[F1](LIST)[1](List)[1][EXE]

??? dimenze matice ???
Vytvoření seznamu (Listu) nebo matice určením počtu buněk (dimenze)
[OPTN]-[LIST]-[Dim]
Postup k určení počtu položek (dimenze) při vytváření seznamu (Listu)
<počet položek n>[![]() ][OPTN][F1](LIST)[2](Dim)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[EXE]
][OPTN][F1](LIST)[2](Dim)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[EXE]
<počet položek n>![]() Dim List <1...20>
Dim List <1...20>
n = 1~255
Vytvoř seznam List 1 o velikosti (dimenzi) pěti buněk s počáteční hodnotou 0
[AC][5][
[F1](LIST)[1](List)[1][EXE]
Nově vytvořený seznam (List) lze zobrazit v módu STAT
Postup vytvoření matice m×n s daným počtem řádků (m) a sloupců (n)
[SHIFT][×]({)<počet řádků m>[,]<počet sloupců n>[SHIFT][![]() ](})[
](})[![]() ]
]
[OPTN][F1](LIST)[2](Dim)[F2](MAT)[1](Mat)[ALPHA]<jméno matice>[EXE]
{<počet řádků m>,<počet sloupců n>}![]() Dim
Mat <jméno matice>
Dim
Mat <jméno matice>
m, n = 1~255
jméno matice ... A~Z
Vytvoř matici A o velikosti 2×3 s hodnotou členů 0
[AC][SHIFT][×]({)[2][,][3][SHIFT][
[OPTN][F1](LIST)[2](Dim)
[F2](MAT)[1](Mat)[ALPHA][X,q,T](A)[EXE]
Vyplnění obsahu všech buněk seznamu (Listu) stejnou
hodnotou
[OPTN]-[LIST]-[Fill]
[OPTN][F1](LIST)[cos](Fill)<hodnota>[,][F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Fill(<hodnota>,List <číslo seznamu (Listu)
1...20>)
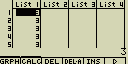
Nahraď obsah všech buněk v seznamu List 1 hodnotou 3
- [AC][OPTN][F1](LIST)[cos](Fill)
[3][,][F1](LIST)[1](List)[1][)][EXE]

- Výsledek:
Vytváření posloupnosti čísel
[OPTN]-[LIST]-[Seq]
[OPTN][F1](LIST)[3](Seq)<výraz>[,]<proměnná>[,]<počáteční
hodnota>[,]<koncová hodnota>[,]<krok>[)][EXE]
Seq <výraz>,<proměnná>,<počáteční
hodnota>,<koncová hodnota>,<krok>)
Výsledek operace se uloží do paměti List Ans nebo je ho možné pomocí ![]() vložit do libovolného seznamu (Listu)
vložit do libovolného seznamu (Listu)
S použitím funkce f(x)=X2 vytvoř posloupnost čísel 12, 62 a 112 s počáteční hodnotou 1, koncovou hodnotou 11 a krokem o velikosti 5
- [OPTN][F1](LIST)[3](Seq)[X,q,T][x2][,][X,q,T][,][1][,][1][1][,][5][)]
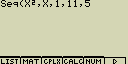
- [EXE]
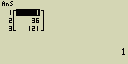
Při zadání koncové hodnoty 12, 13, 14 nebo 15 bude výsledek stejný, protože všechny tyto hodnoty jsou menší než další hodnota přírůstku (16)
Nalezení minima seznamu (Listu)
[OPTN]-[LIST]-[Min]
[OPTN][F1](LIST)[4](Min)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Min(List <číslo seznamu (Listu)
1...20>)
výsledek je možné přiřadit pomocí ![]() do proměnné A~Z, r a q
do proměnné A~Z, r a q
Najdi minimální hodnotu seznamu List 1 (36, 16, 58, 46, 56)
[AC][OPTN][F1](LIST)[4](Min)
[F1](LIST)[1](List)[1][)][EXE]

Nalezení maxima seznamu (Listu)
[OPTN]-[LIST]-[Max]
[OPTN][F1](LIST)[5](Max)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Max(List <číslo seznamu (Listu)
1...20>)
výsledek je možné přiřadit pomocí ![]() do proměnné A~Z, r a q
do proměnné A~Z, r a q
Určení, který ze dvou seznamů (Listů) obsahuje nejmenší hodnotu
[OPTN][F1](LIST)[4](Min)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[,][F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Min(List <číslo seznamu (Listu)
1...20>,číslo seznamu (Listu)
1...20>)
- Výsledek bude uložen v paměti List Ans nebo je ho možné pomocí
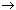 vložit do libovolného seznamu (Listu)
vložit do libovolného seznamu (Listu) - Pokud oba seznamy (Listy) obsahují stejnou nejmenší hodnotu, je jako výsledek uveden první seznam (List)
- Oba seznamy (Listy) musí obsahovat stejný počet položek (buněk),
jinak nastane chyba

Urči, který ze seznamů (List 1 (75, 16, 98, 46, 56), List 2 (35, 59, 58, 72, 67)) obsahuje nejmenší hodnotu
- [AC][OPTN][F1](LIST)[4](Min)
[F1](LIST)[1](List)[1][,]
[F1](LIST)[1](List)[2][)]

- [EXE]
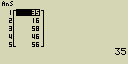
Určení, který ze dvou seznamů (Listů) obsahuje největší hodnotu
[OPTN][F1](LIST)[5](Max)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[,][F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Max(List <číslo seznamu (Listu)
1...20>,číslo seznamu (Listu)
1...20>)
- Ostatní informace jsou stejné jako u určení minima
Aritmetický průměr (střední
hodnota) hodnot v seznamu (Listu)
[OPTN]-[LIST]-[Mean]
[OPTN][F1](LIST)[6](Mean)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Mean(List <číslo seznamu (Listu)
1...20>)
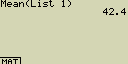
Urči střední hodnotu seznamu List 1 (36, 16, 58, 46, 56)
[OPTN][F1](LIST)[6](Mean)
[F1](LIST)[1](List)[1][)][EXE]
Vážený průměr (střední hodnota s určenou četností
výskytu) hodnot v seznamu (Listu)
[OPTN]-[LIST]-[Mean]
[OPTN][F1](LIST)[6](Mean)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[,][F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Mean(List <číslo seznamu (Listu)
1...20>,List <číslo seznamu (Listu)
1...20>)
- Tato procedura používá dvou seznamů (Listů) z nichž první obsahuje hodnoty a druhý váhy (četnost výskytu)
- Oba seznamy (Listy) musí mít stejný počet položek (buněk)
Urči vážený průměr hodnot v seznamu List 1 (36, 16, 58, 46, 56) přičemž váhy (četnost výskytu) jednotlivých položek jsou zadány v seznamu List 2 (75, 89, 98, 72, 67)
[AC][OPTN][F1](LIST)[6](Mean)
[F1](LIST)[1](List)[1][,]
[F1](LIST)[1](List)[2][)][EXE]

Určení mediánu (hodnota ležící
uprostřed seznamu) hodnot v seznamu (Listu)
[OPTN]-[LIST]-[Median]
[OPTN][F1](LIST)[7](Median)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Median(List <číslo seznamu (Listu)
1...20>)
Urči medián hodnot v seznamu List 1 (36, 16, 58, 46, 56)
[OPTN][F1](LIST)[7](Median)
[F1](LIST)[1](List)[1][)][EXE]

Určení mediánu hodnot s určenou četností výskytu
[OPTN]-[LIST]-[Median]
[OPTN][F1](LIST)[7](Median)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[,][F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Median(List <číslo seznamu (Listu)
1...20>,List <číslo seznamu (Listu)
1...20>)
- Tato procedura používá dvou seznamů (Listů) z nichž první obsahuje hodnoty a druhý váhy (četnost výskytu)
- Oba seznamy (Listy) musí mít stejný počet položek (buněk)
Urči medián hodnot v seznamu List 1 (36, 16, 58, 46, 56) přičemž četnost výskytu (váhy) jednotlivých položek jsou zadány v seznamu List 2 (75, 89, 98, 72, 67)
[OPTN][F1](LIST)[7](Median)
[F1](LIST)[1](List)[1][,]
[F1](LIST)[1](List)[2][)][EXE]
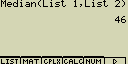
Určení součtu všech hodnot v seznamu (Listu)
[OPTN]-[LIST]-[Sum]
[OPTN][F1](LIST)[8](Sum)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Sum List <číslo seznamu (Listu)
1...20>
Urči součet hodnot v seznamu List 1 (36, 16, 58, 46, 56)
[AC][OPTN][F1](LIST)[8](Sum)
[F1](LIST)[1](List)[1][)][EXE]

Určení součinu všech hodnot v seznamu (Listu)
[OPTN]-[LIST]-[Prod]
[OPTN][F1](LIST)[9](Prod)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Prod List <číslo seznamu (Listu)
1...20>
Urči součin všech hodnot v seznamu List 1 (2, 3, 6, 5, 4)
[OPTN][F1](LIST)[9](Prod)
[F1](LIST)[1](List)[1][)][EXE]

Určení úhrnné četnosti výskytu
(postupného součtu) hodnot v seznamu
(Listu)
[OPTN]-[LIST]-[Cuml]
[OPTN][F1](LIST)[X,q,T](Cuml)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Cuml List <číslo seznamu (Listu)
1...20>
- Výsledek bude uložen v paměti List Ans nebo je ho možné pomocí
 vložit do libovolného seznamu (Listu)
vložit do libovolného seznamu (Listu)
Urči úhrnnou četnost výskytu dat v seznamu List 1 (2, 3, 6, 5, 4)
- [AC][OPTN][F1](LIST)[X,q,T](Cuml)
[F1](LIST)[1](List)[1][)][EXE]

- Výsledek:
2+3 = 5
2+3+6 = 11
2+3+6+5 = 16
2+3+6+5+4 = 20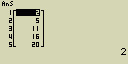
Určení procentuálního zastoupení jednotlivých
položek seznamu (Listu) ku celku
[OPTN]-[LIST]-[%]
[OPTN][F1](LIST)[log](%)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Percent List <číslo seznamu (Listu)
1...20>
- Funkce vypočte procentuelní zastoupení jednotlivých položek seznamu (Listu) vůči celku seznamu (Listu)
- Výsledek bude uložen v paměti List Ans nebo je ho možné pomocí
 vložit do libovolného seznamu (Listu)
vložit do libovolného seznamu (Listu)
Urči procentuelní zastoupení položek v seznamu List 1 (2, 3, 6, 5, 4)
-
[OPTN][F1](LIST)[log](%)
[F1](LIST)[1](List)[1][)]

- [EXE]
2/(2+3+6+5+4)×100 = 10
3/(2+3+6+5+4)×100 = 15
6/(2+3+6+5+4)×100 = 30
5/(2+3+6+5+4)×100 = 25
4/(2+3+6+5+4)×100 = 20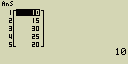
Určení rozdílu mezi sousedními prvky seznamu
(Listu)
[OPTN]-[LIST]-[![]() List]
List]
[OPTN][F1](LIST)[ln](![]() List)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
List)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
![]() List <číslo seznamu (Listu)
1...20>
List <číslo seznamu (Listu)
1...20>
- Počet položek v seznamu
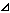 List
je o jednu menší než v seznamu (Listu) původním
List
je o jednu menší než v seznamu (Listu) původním - Výsledek bude uložen v paměti List Ans nebo je ho možné pomocí
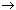 vložit do libovolného seznamu (Listu)
vložit do libovolného seznamu (Listu) - Pokud tuto funkci použiješ na seznam (List) který má jednu nebo žádnou
položku, objeví se chyba

Urči rozdíly mezi sousedními prvky seznamu List 1 (1, 3, 8, 5, 4)
- [AC][OPTN][F1](LIST)[ln](
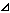 List)
List)
[F1](LIST)[1](List)[1][)]
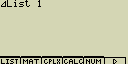
- [EXE]
3-1 = 2
8-3 = 5
5-8 = -3
4-5 = -1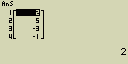
Sloučení dvou seznamů (Listů)
[OPTN]-[LIST]-[Augmnt]
[OPTN][F1](LIST)[sin](Augmnt)[F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[,][F1](LIST)[1](List)<číslo seznamu (Listu)
1...20>[)][EXE]
Augment(List <číslo seznamu (Listu)
1...20>,List <číslo seznamu (Listu)
1...20>)
- Tato funkce umožňuje sloučit dva seznamy (Listy) do jednoho
- Výsledek bude uložen v paměti List Ans nebo je ho možné pomocí
 vložit do libovolného seznamu (Listu)
vložit do libovolného seznamu (Listu)
Sluč seznamy List 1 (-3, -2) a List 2 (1, 9, 10)
- [AC][OPTN][F1](LIST)[sin](Augmnt)
[F1](LIST)[1](List)[1][,]
[F1](LIST)[1](List)[2][)]

- [EXE]
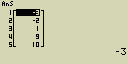
Převedení obsahu seznamu (Listu) do matice
[OPTN]-[LIST]-[L![]() Mat]
Mat]
[OPTN][F1](LIST)[tan](L![]() Mat)<výčet
seznamů (Listů)>[)][EXE]
Mat)<výčet
seznamů (Listů)>[)][EXE]
L![]() Mat(<výčet
seznamů (Listů)>)
Mat(<výčet
seznamů (Listů)>)
- <výčet seznamů (Listů)> ... čísla jednotlivých seznamů (Listů) (ve tvaru List n) oddělená čárkou
- Je možné zadat jeden až všechny seznamy (Listy)
- Seznamy (Listy) tvoří postupně sloupce matice v tom pořadí, v jakém jsou zadány ve výčtu
- Všechny seznamy (Listy) musí mít stejný počet položek (buněk)
- Výsledek bude uložen v paměti Mat Ans nebo je ho možné pomocí
 vložit do libovolné matice
vložit do libovolné matice
Převeď seznamy List 1 (2, 3, 6, 5, 4) a List 2 (11, 12, 13, 14, 15) do matice
-
[OPTN][F1](LIST)[tan](L
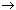 Mat)
Mat)
[F1](LIST)[1](List)[1][,]
[F1](LIST)[1](List)[2][)]

- [EXE]
3-3 Použití seznamu (Listu) ve výpočtu
Výsledky výpočtů jsou implicitně uloženy v paměti List Ans

Chybová hlášení
- U výpočtů se dvěmi seznamy (Listy) může nastat chyba, pokud použiješ seznamy (Listy) s rozdílným počtem prvků
- Chybu může též vyvolat matematická chyba
Vložení seznamu (Listu) do výpočtu
Existují dvě možnosti jak zadat seznam (List) do výpočtu:
1) Zadání seznamu (Listu) podle jména
- Stiskem klávesy [OPTN] vyvolej menu option

- Stiskem [F1](LIST) vyvoláš nabídku pro práci se seznamy (listy)
- Po stisknutí klávesy [1](List) se zobrazí příkaz List za který doplníš číslo seznamu (Listu)
2) Přímé zadání seznamu (Listu) pomocí hodnot
Seznam (List) lze zadat také přímo pomocí výčtu hodnot uzavřeném ve složené
závorce ({}) oddělených čárkou (,)
Vytvoř seznam (List) zadáním hodnot 56, 82 a 64
- [SHIFT][×]({)[5][6][,][8][2][,][6][4][SHIFT][
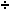 ](})
](})
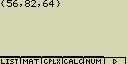
- [EXE]
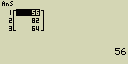
Vynásob seznam List 3 (41, 65, 22) seznamem (6, 0, 4)
- [OPTN][F1](LIST)[1](List)[3][×][SHIFT][×]({)[6][,][0][,][4][SHIFT][
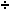 ](})
](})
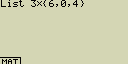
- [EXE]

Přiřazení obsahu jednoho seznamu (Listu) do jiného seznamu (Listu)
Pro přiřazení obsahu jednoho seznamu (Listu) do druhého použij klávesu [![]() ]
]
Přiřaď obsah seznamu List 3 do seznamu List 1
[OPTN][F1](LIST)[1](List)[3][

Zadání [OPTN][F1](LIST)[1](List)[3] může být nahrazeno jako [SHIFT][×]({)[4][1][,][6][5][,][2][2][SHIFT][
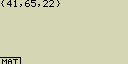
Přiřaď obsah seznamu List Ans do seznamu List 1
[OPTN][F1](LIST)[1](List)[SHIFT][(-)](Ans)[
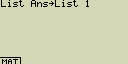
Zobrazení hodnoty z určité buňky seznamu (Listu) (adresování buněk)
Ze seznamu (Listu) lze získat číslo z určité buňky a použít je ve výpočtu.
Číslo požadované buňky se zadává do uzavřených hranatých závorek
Vypočti sinus hodnoty ve třetí buňce seznamu List 2
[sin][OPTN][F1](LIST)[1](List)[2][SHIFT][+]([)[3][SHIFT][-](])[EXE]

Vložení hodnoty do určité buňky seznamu (Listu)
Do seznamu (Listu) lze na jakoukoliv pozici zapsat libovolné číslo (předchozí
hodnota se přitom přepíše). Podmínkou je, aby předchozí buňky nebyly prázdné
Do buňky 23 v seznamu List 2 vlož číslo 25
[2][5][

Zobrazení obsahu seznamu (Listu)
Zobraz obsah seznamu List 1
[OPTN][F1](LIST)[1](List)[1][EXE]

- Tato operace zobrazí obsah seznamu (Listu) a umístí jej do seznamu List Ans. Obsah seznamu List Ans můžeš přímo použít v dalším výpočtu
Použití obsahu paměti List Ans ve výpočtu
Vynásob obsah seznamu List Ans číslem 36
[OPTN][F1](LIST)[1](List)[SHIFT][(-)](Ans)[×][3][6][EXE]
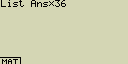
- Operace [OPTN][F1](LIST)[1](List)[SHIFT][(-)](Ans) vyvolá obsah paměti List Ans
- Tato operace přepíše současný stav paměti List Ans novým výsledkem
Grafy funkcí s použitím seznamu (Listu)
Pokud chceš nakreslit grafy více funkcí, lze zadat například funkci Y1=
List 1X
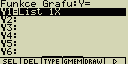
Pokud bude seznam List 1 obsahovat hodnoty 1, 2 a 3, bude tento zápis představovat
tři grafy Y=X, Y=2X a Y=3X
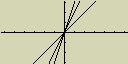
Pro použití seznamů (Listů) s funkcemi grafů ale platí určitá omezení
Zápis výsledků výpočtů do seznamu (Listu)
K zápisu hodnot představujících výsledky výpočtů do seznamu (Listu) lze
použít funkce pro tvorbu tabulek z módu GRPH.TBL.
Nejprve musíš vytvořit tabulku hodnot
a poté převést její obsah do seznamu
(Listu)
Seznamy (Listy) ve vzorcích
Seznamy (Listy) mohou být použity ve výpočtech stejně jako číselné
hodnoty. Pokud je poté výsledkem výpočtu seznam (List), uloží se do paměti
List Ans
Vypočti sinus hodnot uložených v seznamu List 3 (41, 65, 22) (úhlová míra radiány)
- [sin][OPTN][F1](LIST)[1](List)[1]

- [EXE]
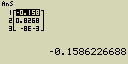
Zadání [sin][OPTN][F1](LIST)[1](List)[1] může být nahrazeno jako
[sin][SHIFT][×]({)[4][1][,][6][5][,][2][2][SHIFT][![]() ](})
](})
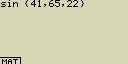
Použij seznamy List 1 (1, 2, 3) a List 2 (4, 5, 6) pro výpočet List 1List 2
Výsledkem budou hodnoty 14, 25 a 36
- [OPTN][F1](LIST)[1](List)[1][^][OPTN][F1](LIST)[1](List)[2]
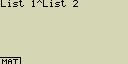 nebo také
nebo také 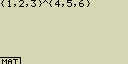
- [EXE]

3-4 Přepínání mezi soubory seznamů
V každém souboru (File 1 až File 6) můžeš uložit až 20 seznamů
(Listů)
Přepínání mezi soubory seznamů (Listů)
- V módu STAT stiskni [CTRL][F3](SET UP)
- Pomocí kurzorových šipek najeď na položku "List File", stiskni [F1](FILE) a zadej číslo souboru seznamů, který chceš zvolit jako aktivní
Přepnutí na soubor seznamů (Listů) číslo 3
- [CTRL][F3](SET UP)

- [F1](FILE)[3]

- [EXE]
Všechny následující operace se seznamy (Listy) se budou provádět v aktivním souboru
Statistické výpočty a grafy
Tato kapitola se zabývá zadáním statistických dat do seznamu (Listu) a následným
zpracováním těchto dat (výpočtem regresí a statistických hodnot)
Tato kapitola obsahuje řadu obrázků grafů. U každého z nich byly za účelem zobrazení charakteristických vlastností zadány nové vstupní hodnoty. Proto pokud se pokusíš vytvořit podobný graf, použiješ skoro jistě jiné hodnoty což způsobí, že tvé grafy se budou od těch v tomto manuálu lišit
6-1 Příprava dat
Z hlavního menu vstup do módu STAT. Pro práci se statistickými daty se budou
používat seznamy (Listy) se statistickými údaji. V seznamu (Listu) se jde
pohybovat pomocí kurzorových kláves ![]() ,
,
![]() ,
,
![]() a
a ![]() . Ve statistických výpočtech nejde
používat komplexní čísla
. Ve statistických výpočtech nejde
používat komplexní čísla

Zadání dat do seznamu (Listu)
Zadej následující skupiny dat:
0.5, 1.2, 2.4, 4.0, 5.2
-2.1, 0.3, 1.5, 2.0, 2.4
[1][.][2][EXE][2][.][4][EXE]
[4][EXE][5][.][2][EXE]
[0][.][3][EXE][1][.][5][EXE]
[2][EXE][2][.][4][EXE]

Pokud jsou zadána vstupní data, můžeš je použít pro statistické výpočty
Změna parametrů grafu
Pomocí těchto procedur lze nastavit, jestli se má graf kreslit, typ grafu a
jiná nastavení pro každý graf z menu grafů (GPH1, GPH2, GPH3)
Menu grafů vyvoláš stiskem [F1](GRPH)
Menu obsahuje tyto položky:
- S-Gph1 ... vykreslení prvního statistického grafu*1
- S-Gph2 ... vykreslení druhého statistického grafu*1
- S-Gph3 ... vykreslení třetího statistického grafu*1
- Select ... volba současného zobrazení více grafů (GPH1, GPH2, GPH3)
- Set ... nastavení grafu (typ, seznamy (Listy) se vstupními údaji a podobně)
- *1 Původní nastavení typu grafu je u všech tří grafů nastaveno na graf rozložení, ale lze ho změnit na jiný typ
- Pro jednotlivé grafy lze určit, zda se mají nebo nemají vykreslovat
1) Hlavní nastavení grafu
[GRPH]-[Set]
Popis základního nastavení pro každý graf (GPH1, GPH2, GPH3)
- Typ grafu
Původní nastavení typu grafu je u všech tří grafů nastaveno na graf rozložení, ale lze ho změnit na jiný typ - Seznam (List)
Původní nastavení seznamu (Listu) statistických dat s jednou proměnnou je seznam List 1 a pro seznam (List) se dvěmi proměnnými List 1 a List 2
Mimo to si můžeš nastavit, které seznamy (Listy) se použijí jako zdroj dat pro hodnoty x, y a četnost - Četnost
Běžně je jeden nebo dvojice (pár) údajů v grafu reprezentován jako bod. Pokud však pracuješ s velkým počtem položek, mohou nastat potíže v tom, že graf obsahuje velké množství údajů. pokud toto nastane, je vhodnější nadefinovat k opakující se hodnotě údaj o počtu výskytů (četnosti) a tak zaznamenat hned několik hodnot najednou. Graf je pak i lépe čitelný
Jako četnost se zadávají pouze celá kladná čísla, jiné hodnoty způsobí chybu - Typ značky
Umožňuje nastavit tvar bodů na grafu
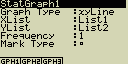
Zobrazení displeje s hlavním nastavením grafu
Nastavení zobrazíš stiskem [F1](GRPH)[5](Set)
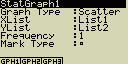
Následuje celkový přehled nastavení. Nastavení u jednotlivých grafů se může
lišit
- StatGraph ... určení statistického grafu
- GPH1 ... první statistický graf
- GPH2 ... druhý statistický graf
- GPH3 ... třetí statistický graf
- Graph Type ... určení typu grafu
- Scat ... schema rozložení
- xy ...xy spojnicový graf
- NPP ... normální pravděpodobnost
- Hist ... histogram (sloupcový graf)
- Box ... graf rozložení
- ModB ... modifikovaný graf rozložení
- N.Dis ... normální rozdělení
- Brkn ... čárový graf
- X ... lineární regrese
- Med ... regrese Med-Med
- X^2 ... kvadratická regrese
- X^3 ... kubická regrese
- X^4 ... kvartická regrese
- Log ... logaritmická regrese
- Exp ... exponenciální regrese
- Pwr ... mocninná regrese
- Sin ... sinová regrese
- Lgst ... logistická regrese
- XList ... data na ose X
- LIST ... seznam List 1 až 20
- YList ... data na ose Y
- LIST ... seznam List 1 až 20
- Frequency ... četnost výskytu hodnoty
- 1 ... stejná četnost pro všechny položky
- LIST ... seznam List 1 až 20. Četnost výskytu dat v Listu X a Y
- Mark Type ... vzhled bodů v grafu
2) Nastavení (ne)zobrazení grafu
[GRPH]-[Select]
Následující nastavení určuje, který ze statistických grafů se
(ne)vykreslí
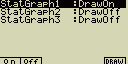
- Stiskem [F1](GRPH)[4](Select) zobrazíš nastavení zobrazení statistických grafů
- Pomocí kurzorových kláves označ graf jehož nastavení chceš změnit
a stiskni příslušnou funkční klávesu
[F1] - On ... povolit vykreslení
[F2] - Off ... zakázat vykreslení
[F6] - DRAW ... okamžité vykreslení povolených grafů - Stiskem [ESC] nastavení opustíš
- Parametry V-Window se u statistického grafu nastavují automaticky. Pokud chceš tyto údaje upravit ručně, musíš v menu SET UP u položky „Stat Wind” nastavit parametr „Manual” (Jakmile máš zobrazen seznam dat, stiskni [CTRL][F3](SET UP)[F2](Man)[ESC])
- původní nastavení používá pro data x seznam List 1 a pro data y seznam List 2. Každý soubor hodnot x/y je v grafu rozložení reprezentován bodem
- Pokud stiskneš při zobrazeném statistickém grafu [CTRL][0], dolní menu se neskryje
6-2 Zpracování dat s jednou proměnnou x
Data s jednou proměnnou si lze přiblížit na příkladu školní třídy.
Pokud chceš spočítat průměrnou výšku žáka, zpracováváš pouze jednu
proměnnou (výšku všech žáků třídy)
Před vykreslením grafu můžeš nastavit jeho parametry jak bylo popsáno v
minulé kapitole
Následující typy grafů jsou dostupné při řešení statistických výpočtů
s jednou proměnnou
Graf normální pravděpodobnosti (NPP)
Zachycuje poměr proměnné a normálního rozdělení. Očekávané hodnoty
normálního rozdělení jsou vyneseny na svislé ose (Y), zadané hodnoty jsou
vyneseny na ose vodorovné (X)
XList ... seznam (List) se vstupními daty
Mark ... tvar značky, která bude zobrazena v grafu
Po stisknutí [ESC] nebo [SHIFT][ESC](QUIT) se vrátíš do základní nabídky
módu STAT
Histogram (sloupcový graf) (Hist)
XList ... seznam (List) se vstupními daty
Frequency ... četnost výskytu jednotlivých položek. Nastavuje se
hodnota 1 (stejná četnost pro všechny položky(= stejná výška sloupců
grafů)) nebo List n (četnosti jednotlivých položek (= výšky
jednotlivých sloupců grafu))

Možnost nastavení začátku vykreslování a šířky sloupců. Po stisknutí
[EXE] se graf vykreslí

Graf rozložení (Box)
Zvláštní typ grafu z něhož lze odečíst složení množiny hodnot. oblast
uvnitř obdelníku označuje oblast dat od 25% do 75%. Dělící čára uvnitř
obdelníku označuje hranici 50%. Vodorovné čáry vedoucí z obdelníku označují
minimální a maximální hodnoty zadaných dat
XList ... seznam (List) se vstupními daty
Frequency ... četnost výskytu jednotlivých položek. Nastavuje se
hodnota 1 (stejná četnost pro všechny položky) nebo List n (četnosti
jednotlivých položek)
Modifikovaný graf rozložení (ModB)
Tento graf zanedbá všechny hodnoty mimo oblast 1.5 × IQR (IQR = Q3 - Q1 kde
Q1 první čtvrtina a Q3 je třetí čtvrtina) a z této vybrané množiny
vykreslí obdobný graf jako v předchozím případě. původní hranice se
zobrazí jako body
XList ... seznam (List) se vstupními daty
Frequency ... četnost výskytu jednotlivých položek. Nastavuje se
hodnota 1 (stejná četnost pro všechny položky) nebo List n (četnosti
jednotlivých položek)
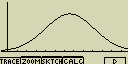
Normální rozdělení (N.Dis)
Pro vykreslení grafu normálního rozdělí se používá následující
funkce:
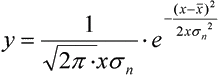
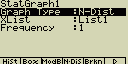
XList ... seznam (List) se vstupními daty
Frequency ... četnost výskytu jednotlivých položek. Nastavuje se
hodnota 1 (stejná četnost pro všechny položky) nebo List n (četnosti
jednotlivých položek)
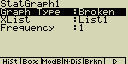
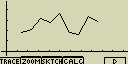
Čárový graf (Brkn)
Úsečky spojují body které jsou středem vršku sloupce histogramu (sloupcového
grafu)
XList ... seznam (List) se vstupními daty
Frequency ... četnost výskytu jednotlivých položek. Nastavuje se
hodnota 1 (stejná četnost pro všechny položky) nebo List n (četnosti
jednotlivých položek)

Možnost nastavení začátku vykreslování a šířky sloupců. Po stisknutí
[EXE] se graf vykreslí
Zobrazení výsledků výpočtů statistických hodnot s jednou proměnnou
Statistika může být vyjádřena i hodnotami parametrů. pokud je zobrazen
statistický graf, pak po stisknutí [F4](CALC)[1](1VAR) se vypočtou následující
hodnoty

Pomocí kurzorových šipek je možné v seznamu listoval
Význam jednotlivých parametrů:
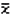 ... průměr dat
... průměr dat- Sx ... součet prvků
- Sx2 ... součet čtverců
- xsn ... střední kvadratická chyba (směrodatná odchylka)*1
- xsn-1 ... empirická jednotková střední chyba jednoho měření (odhad rozptylu)*2
- n ... počet prvků
- minX ... minimální hodnota
- Q1 ... první čtvrtina
- Med ... medián (hodnota uprostřed souboru dat)
- Q3 ... třetí čtvrtina
- maxX ... maximální hodnota
- Mod ... modus (hodnota s největší četností výskytu)
- Mod:n ... počet prvků v modu*3
- Mod:F ... počet prvků s největší četností výskytu
- *1
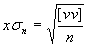
kde v jsou odchylky jednotlivých hodnot od průměru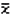
[] je symbol pro sumu - *2
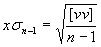
- empirická jednotková střední chyba výsledku (průměru ze vstupních
hodnot)
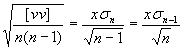
- *3Pokud je výsledkem modu více řešení, jsou zobrazena všechna
Po stisknutí [F6](DRAW) dojde k návratu na displej s vykresleným statistickým grafem
6-3 Zpracování dat s dvěmi proměnnými x a y
Vykreslení schema rozložení (scat) a xy spojnicového grafu
(xy)
Popis
Následujícím postupem vytvoříš schema rozložení a jeho body propojíš
pomocí xy spojnicového grafu
- Vstup do módu STAT
- Do seznamů (Listů) zadej data
- Nastav jestli chceš vykreslit schema rozložení (vynést body) nebo xy spojnicový graf a nechej graf vykreslit
Do seznamu statistických hodnot se vrátíš stiskem [ESC] nebo [SHIFT][ESC](QUIT)
Zadej dvě množiny dat:
0.5, 1.2, 2.4, 4.0, 5.2
-2.1, 0.3, 1.5, 2.0, 2.4
Nejprve vykresli schema rozložení a poté xy spojnicový graf
Postup:
Regresní grafy
Popis
V následujícím příkladě zadáš data se dvěmi proměnnými a provedeš výpočet
regrese. Výsledky poté vyneseš do grafu
- Vstup do módu STAT
- Do seznamů (Listů) zadej data a vykresli schema rozložení
- Zvol typ regrese a proveď výpočet regresních koeficientů
- Vykresli graf regrese
- V regresním grafu je možné krokování grafu
Zadej dvě množiny dat:
0.5, 1.2, 2.4, 4.0, 5.2
-2.1, 0.3, 1.5, 2.0, 2.4
Nejprve vykresli schema rozložení a poté proveď logaritmickou regresi, zobraz vypočtené regresní koeficienty a vykresli regresní graf
Postup:
- [MENU] STAT
-
[0][.][5][EXE][1][.][2][EXE]
[2][.][4][EXE][4][EXE][5][.][2][EXE]
[(-)][2][.][1][EXE][0][.][3][EXE]
[1][.][5][EXE][2][EXE][2][.][4][EXE]
[F1](GRPH)[5](Set) [F1](Scat)[ESC]
[F1](Scat)[ESC]
[F1](GRPH)[1](S-Gph1)
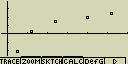
-
[F4](CALC)[7](Log)

-
[F6](DRAW)
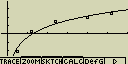
Výběr typu regrese
Poté co vykreslíš graf pro statistická data dvou proměnných x/y, stiskni
[F4](CALC) a vyber typ regrese:
- 2VAR ... výpočty statistických hodnot se dvěmi proměnnými
- Linear ... lineární regrese
- MedMed ... regrese Med-Med
- Quad ... kvadratická regrese
- Cubic ... kubická regrese
- Quart ... kvartická regrese
- Log ... logaritmická regrese
- Exp ... exponenciální regrese
- Power ... mocninná regrese
- Sin ... sinová regrese
- Lgstic ... logistická regrese
Zobrazení výsledků statistických výpočtů
Pokaždé když spočítáš regresi, objeví se na displeji parametry regresního
modelu (např. parametry a, b pro lineární regrese y=ax+b)
Parametry regrese se vypočtou okamžitě poté, co zvolíš typ regrese
Grafické zpracování výsledků
Jakmile se zobrazí parametry regresního modelu, můžeš stisknutím
[F6](DRAW) zobrazit odpovídající graf
Lineární regrese
Lineární regrese používá metody nejmenších čtverců pomocí které proloží
původním grafem přímku tak, aby se její průběh co nejvíce blížil rozložení
bodů
Případné nastavení pro statistický graf:
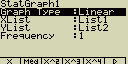
[F4](CALC)[2](Linear)
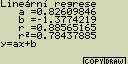
[F6](DRAW)
vzorec pro model lineární regrese
y=ax+b
a ... regresní koeficient (sklon)
b ... regresní koeficient (y pro x=0)
r ... korelační koeficient
r2 ... směrodatná odchylka
Regrese Med-Med
Pokud se v množině hodnot nachází velké množství extrémních hodnot, je
vhodnější zvolit tuto metodu místo metody nejmenších čtverců (lineární
regrese). Výsledek je podobný lineární regrese ale minimalizuje se vliv
extrémů
Případné nastavení pro statistický graf:
[F4](CALC)[3](MedMed)
[F6](DRAW)
vzorec pro model Med-Med
y=ax+b
a ... regresní koeficient (sklon)
b ... regresní koeficient (y pro x=0)
Kvadratická regrese
Tento typ regrese pomocí metody nejmenších čtverců proloží zadanými body
polynom druhého stupně
Případné nastavení pro statistický graf:
[F4](CALC)[4](Quad)
[F6](DRAW)
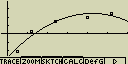
vzorec pro model kvadratické regrese
y=ax2+bx+c
a ... regresní koeficient s druhou mocninou
b ... regresní koeficient s třetí mocninou
c ... konstanta v regresním výrazu (y pro x=0)
Kubická regrese
Tento typ regrese pomocí metody nejmenších čtverců proloží zadanými body
polynom třetího stupně
Případné nastavení pro statistický graf:
[F4](CALC)[5](Cubic)

[F6](DRAW)
vzorec pro model
y=ax3+bx2+cx+d
a ... regresní koeficient se třetí mocninou
b ... regresní koeficient s druhou mocninou
c ... regresní koeficient s první mocninou
d ... konstanta v regresním výrazu (y pro x=0)
Kvartická regrese
Tento typ regrese pomocí metody nejmenších čtverců proloží zadanými body
polynom čtvrtého stupně
Případné nastavení pro statistický graf:
[F4](CALC)[6](Quart)
[F6](DRAW)
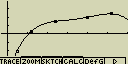
vzorec pro model kvartické regrese
y=ax4+bx3+cx2+dx+e
a ... regresní koeficient se čtvrtou mocninou
b ... regresní koeficient se třetí mocninou
c ... regresní koeficient s druhou mocninou
d ... regresní koeficient s první mocninou
e ... konstanta v regresním výrazu (y pro x=0)
Logaritmická regrese
y je zde logaritmickou funkcí x. Regresní vzorec vypadá y=a+b.ln(x).
Pokud zavedeme substituci X=ln(x), platí y=a+bX což je již známý
vzorec lineární regrese
Případné nastavení pro statistický graf:
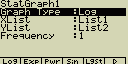
[F4](CALC)[7](Log)

[F6](DRAW)
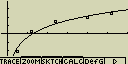
vzorec pro model logaritmické regrese
y=a+b.ln(x)
a ... regresní konstanta
b ... regresní koeficient
r ... korelační koeficient
r2 ... směrodatná odchylka
Exponenciální regrese
y je zde exponenciální funkcí x. Regresní vzorec lze zapsat
jako y=a.ebx. Pokud obě strany této rovnice zlogaritmujeme,
dostaneme vztah ln(y)=ln(a)+bx. Po použití substituce Y=ln(y) a a=ln(a)
opět platí vzorec lineární regrese Y =a+bX
Případné nastavení pro statistický graf:
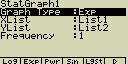
[F4](CALC)[8](Exp)
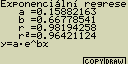
[F6](DRAW)
vzorec pro model exponenciální regrese
y=a.ebx
a ... regresní koeficient
b ... regresní konstanta
r ... korelační koeficient
r2 ... směrodatná odchylka
Mocninná regrese
y je zde mocninnou funkcí x. Regresní vzorec lze zapsat jako y=a.xb.
Pokud obě strany této rovnice zlogaritmujeme, dostaneme vztah ln(y)=ln(a)+b.ln(x).
Po použití substituce X=ln(x) a a=ln(a) opět platí vzorec lineární
regrese y=a+bX
Případné nastavení pro statistický graf:
[F4](CALC)[9](power)

[F6](DRAW)
vzorec pro model mocninné regrese
y=a.xb
a ... regresní koeficient
b ... regresní mocnitel
r ... korelační koeficient
r2 ... směrodatná odchylka
Sinová regrese
Sinová regrese je nejvhodnější pro periodické děje. Pokud kreslíš graf
sinové regrese, nastaví se úhlová míra na radiány (pokud provedeš pouze
číselný výpočet, nastavení se nezmění)
Zpracování dat může trvat poměrně dlouhou dobu
Případné nastavení pro statistický graf:
[F4](CALC)[X,q,T](Sin)
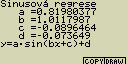
[F6](DRAW)
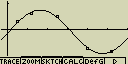
vzorec pro model sinové regrese
y=a.sin(bx+c)+d
Logistická regrese
Logistická regrese je nejvýhodnější pro časové děje u nichž časem
dojde k ustálení (saturaci) časově závislé veličiny
Zpracování dat může trvat poměrně dlouhou dobu
Případné nastavení pro statistický graf:
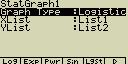
[F4](CALC)[log](Lgstic)

[F6](DRAW)
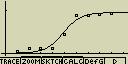
vzorec pro model logistické regrese
![]()
Výpočet zbytku
Vzdálenost mezi body (souřadnicí y) a regresním modelem může být během
výpočtu zjišťována
Zobraz statistická data a v menu SET
UP změň u položky „Resid List” nastavení na List n. Vypočítané
zbytky se poté budou ukládat do tohoto seznamu (Listu)
Počítá se vzdálenost po svislici (y, x=konst) mezi bodem a regresním
modelem
Pokud je bod výš než křivka regresního modelu, je vzdálenost kladná, v
opačném případě je záporná
Výpočet zbytku je možný spočítat a uložit pro všechny regresní modely
- Stará data ve zvoleném seznamu (Listu) se při dalším výpočtu přepíší novými hodnotami. Zbytky se ukládají ve stejném pořadí jako data modelu
Zobrazení výsledků výpočtů statistických hodnot se dvěmi proměnnými
Statistické hodnoty dvou proměnných mohou být vyjádřeny jako grafy a
hodnoty parametrů. Pokud je zobrazen graf, parametry se zobrazí po stisknutí [F4](CALC)[1](2VAR)
Pomocí kurzorových šipek je možné v seznamu listoval
Význam jednotlivých parametrů:
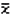 ... průměr dat v seznamu List X
... průměr dat v seznamu List X- Sx ... součet dat v seznamu List X
- Sx2 ... součet čtverců v seznamu List X
- xsn ... střední kvadratická chyba (směrodatná odchylka) dat v seznamu List X*1
- xsn-1 ... empirická jednotková střední chyba jednoho měření (odhad rozptylu) dat v seznamu List X*2
- n ... počet prvků
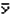 ... průměr dat v seznamu List Y
... průměr dat v seznamu List Y- Sy ... součet dat v seznamu List Y
- Sy2 ... součet čtverců v seznamu List Y
- ysn ... střední kvadratická chyba (směrodatná odchylka) dat v seznamu List Y*1
- ysn-1 ... empirická jednotková střední chyba jednoho měření (odhad rozptylu) dat v seznamu List Y*2
- Sxy ... součet dat v seznamech List X a List Y
- minX ... minimální hodnota v seznamu List X
- maxX ... maximální hodnota v seznamu List X
- minY ... minimální hodnota v seznamu List Y
- maxY ... maximální hodnota v seznamu List Y
- *1
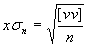
kde v jsou odchylky jednotlivých hodnot od průměru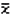
[] je symbol pro sumu
Stejným způsobem probíhá i výpočet pro hodnoty y - *2
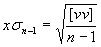
- empirická jednotková střední chyba výsledku (průměru ze vstupních
hodnot)
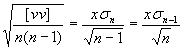
Po stisknutí [F6](DRAW) dojde k návratu na displej s vykresleným
statistickým grafem
Kopírování regresního vzorce do módu GRPH.TBL
Výsledky výpočtu regresního modelu lze přenést do módu
GRPH.TBL
- Vypočti regresní koeficienty

- Po stisknutí [F5](COPY) se zobrazí seznam funkcí grafu

Pomocí kurzorových šipek najeď na pozici, kam chceš vzorec regresního modelu uložit a stiskni [EXE] - Opět se zobrazí vypočtené regresní koeficienty

Do seznamu funkcí grafu se předtím ale vloží vzorec regresního modelu

Současné zobrazení více grafů
V módu STAT jde pomocí změny parametrů (viz. část „Nastavení
(ne)zobrazení grafu”) zobrazit najednou až tři statistické grafy. Toto
nastavení jde provést pro jeden, dva nebo všechny tři statistické grafy přepnutím
na „On”. Poté stiskni [F6](DRAW) a grafy se vykreslí. Po vykreslení si můžeš
vybrat vzorec, který chceš použít pro výpočet regrese
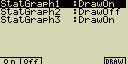
[F4](CALC)
[2](Linear)
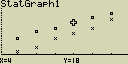
Text v horní části displeje označuje zvolený graf (Označení StatGraph1,
StatGraph2, StatGraph3 zde představují grafy Graph1, Graph2, Graph3 nebo GPH1,
GPH2, GPH3)
- Mezi grafy se dá přeskakovat pomocí kurzorových šipek
 a
a 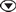
- Pokud máš zvolený graf který chceš použít, stiskni [EXE]
Nyní můžeš pro statistické výpočty pracovat s postupy popsanými výše
v čísti „Zobrazení výsledků výpočtů statistických hodnot se dvěmi proměnnými”
Zobrazení grafu funkce pomocí statistického grafu
Popis
Přes statistický graf funkce dvou proměnných lze zobrazit graf funkce jakéhokoliv
typu
- Vstup do módu STAT
- Zadej údaje a vykresli statistický graf
- Zobraz menu pro grafy funkcí a zadej tvar funkce, kterou chceš překrýt statistický graf
- Vykresli funkci
Zadej dvě množiny dat:
0.5, 1.2, 2.4, 4.0, 5.2
-2.1, 0.3, 1.5, 2.0, 2.4
Nejprve vykresli schema rozložení a poté jej překresli grafem funkce y=2.ln(x)
Postup:
- [MENU] STAT
-
[0][.][5][EXE][1][.][2][EXE]
[2][.][4][EXE][4][EXE][5][.][2][EXE]
[(-)][2][.][1][EXE][0][.][3][EXE]
[1][.][5][EXE][2][EXE][2][.][4][EXE]
[F1](GRPH)[1](S-Gph1)
-
[F5](DefG)

[2][ln][X,q,T][EXE] (uloženo Y1=2.lnx)
-
[F6](DRAW)
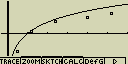
- Grafem funkce jde i krokovat
- Kreslit jde pouze grafy v pravoúhlých souřadnicích
- Stiskneš-li během zadávání funkce klávesu [ESC], vrátí se tvar
funkce na hodnotu před změnou
Pokud stiskneš [SHIFT][ESC](QUIT), smažeš zadávanou funkci a vrátíš se de seznamu se statistickými údaji
6-4 Statistické výpočty
Doposud byly všechny výpočty prováděny až po zobrazení grafu. Následující
procedury mohou být použity pro statistické výpočty i samostatně
Označení seznamu (Listu) s údaji pro statistické výpočty
Před začátkem výpočtu musíš zadat vstupní data a určit, kde jsou uložena
Data nejprve zobraz a poté stiskni [F2](CALC)[4](Set)
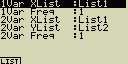
Význam jednotlivých položek:
1Var XList ... umístění statistických hodnot x při výpočtech s
jednou proměnnou (XList)
1Var Freq ... umístění hodnot s četností výskytu statistických
hodnot x při výpočtech s jednou proměnnou (Frequency)
2Var XList ... umístění statistických hodnot x při výpočtech se dvěmi
proměnnými (XList)
2Var XList ... umístění statistických hodnot y při výpočtech se dvěmi
proměnnými (YList)
2Var Freq ... umístění hodnot s četností výskytu statistických
hodnot x a y při výpočtech se dvěmi proměnnými (Frequency)
Výpočty v této sekci jsou prováděny pomocí příkazů
Statistické výpočty s jednou proměnnou
Doposud se statistické parametry počítaly až po zobrazení grafu (od grafu
normální pravděpodobnosti až po čárový graf). Tyto hodnoty lze spočítat i přímo,
pokud při zobrazeném seznamu dat stiskneš [F2](CALC)[1](1VAR)
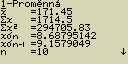
Poté můžeš pomocí kurzorových šipek ![]() a
a ![]() listovat vytvořenou tabulkou. Význam jednotlivých položek je popsán v části
„Zobrazení výsledků výpočtů statistických hodnot s jednou proměnnou”
listovat vytvořenou tabulkou. Význam jednotlivých položek je popsán v části
„Zobrazení výsledků výpočtů statistických hodnot s jednou proměnnou”
Statistické výpočty se dvěmi proměnnými
Doposud se statistické parametry počítaly až po zobrazení grafu (od lineární
až po logistickou regresi). Tyto hodnoty lze spočítat i přímo,
pokud při zobrazeném seznamu dat stiskneš [F2](CALC)[2](2VAR)
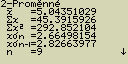
Poté můžeš pomocí kurzorových šipek ![]() a
a ![]() listovat vytvořenou tabulkou. Význam jednotlivých položek je popsán v části
„Zobrazení výsledků výpočtů statistických hodnot se dvěmi proměnnými”
listovat vytvořenou tabulkou. Význam jednotlivých položek je popsán v části
„Zobrazení výsledků výpočtů statistických hodnot se dvěmi proměnnými”
Výpočet regrese
Doposud se statistické parametry počítaly až po zobrazení grafu (od lineární
až po logistickou regresi)
Každý regresní model byl vyjádřen rovnicí a regresními parametry. Tyto
parametry je možné spočítat i přímo a to po stisknutí [F2](CALC)[3](REG)
kdy se objeví rozbalovací menu s těmito položkami:
- Linear ... lineární regrese
- MedMed ... regrese Med-Med
- Quad ... kvadratická regrese
- Cubic ... kubická regrese
- Quart ... kvartická regrese
- Log ... logaritmická regrese
- Exp ... exponenciální regrese
- Power ... mocninná regrese
- Sin ... sinová regrese
- Lgstic ... logistická regrese
Urči parametry lineární regrese
[F2](CALC)[3](REG)[1](Linear)
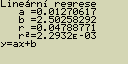
Význam zobrazených parametrů je popsán v částech věnovaných lineární až logistické regresi
Odhad hodnot (![]() ,
,![]() )
)
Po vykreslení statistického grafu v módu STAT je možné v módu RUN.MAT vypočítat odhad parametrů regresního grafu x a y
Spočítej lineární regrese podle uvedené tabulky a s použitím uvedených údajů urči
| xi | yi |
| 10 | 1003 |
| 15 | 1005 |
| 20 | 1010 |
| 25 | 1011 |
| 30 | 1014 |
- Vstup do módu STAT
- Zadej údaje uvedené v tabulce a nakresli graf lineární regrese

- Vstup do módu RUN.MAT
- Zadej:
[2][0] (hodnota xi)
[OPTN][F6](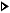 )[F4](STAT)[2](
)[F4](STAT)[2](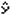 )[EXE]
(zobrazí se odhad hodnoty
)[EXE]
(zobrazí se odhad hodnoty 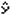 i
pro xi=20
i
pro xi=20
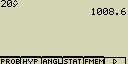
[1][0][0][0] (hodnota yi)
[F4](STAT)[1](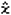 )[EXE]
(zobrazí se odhad hodnoty
)[EXE]
(zobrazí se odhad hodnoty 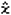 i
pro yi=1000
i
pro yi=1000
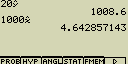
- Odhad nelze získat pro regrese Med-Med, kvadratickou, kubickou, kvartickou, logaritmickou, exponenciální mocninou, sinovou a logistickou regresi (= jde určit pouze u lineární regrese)
Výpočet rozdělení pravděpodobnosti
V módu RUN.MAT je možné spočítat rozdělení
pravděpodobnosti pro jednu proměnnou
Po stisknutí [OPTN][F6](![]() )[F1](PROB)
se zobrazí menu s těmito položkami:
)[F1](PROB)
se zobrazí menu s těmito položkami:
- P( ... odhad pravděpodobnosti P(t)
- Q( ... odhad pravděpodobnosti Q(t)
- R( ... odhad pravděpodobnosti R(t)
- t( ... normalizovaná výchylka t(x)
Tyto hodnoty se počítají podle následujících vzorců:
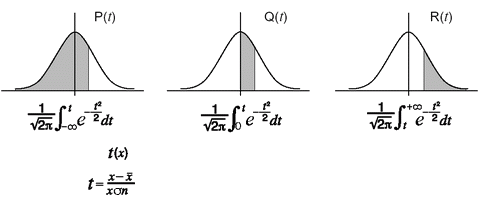
Následující tabulka zachycuje výsledky měření výšky 20ti studentů. Zjisti jaká část studentů má v % výšku v rozmezí 160.5 až175.5 cm a dále kolik % studentů má výšku rovnou nebo větší než 175.5 cm
| pořadí | výška [cm] | četnost |
| 1 | 158.5 | 1 |
| 2 | 160.5 | 1 |
| 3 | 163.3 | 2 |
| 4 | 167.5 | 2 |
| 5 | 170.2 | 3 |
| 6 | 173.3 | 4 |
| 7 | 175.5 | 2 |
| 8 | 178.6 | 2 |
| 9 | 180.4 | 2 |
| 10 | 186.7 | 1 |
- Údaje o výšce zadej do seznamu List 1, údaje o četnosti do seznamu List 2
- Zadej:
[F2](CALC)[4](Set)
 [F2](LIST)[2][EXE]
[F2](LIST)[2][EXE]
[ESC]
[F2](CALC)[1](1VAR)
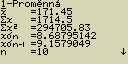
- Vstup do módu RUN.MAT a zadej:
[OPTN][F6](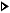 )
dále budou probíhat výpočty pravděpodobnosti
)
dále budou probíhat výpočty pravděpodobnosti
[F1](PROB)[8](t()[1][6][0][.][5][)][EXE]
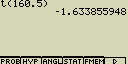
[F1](PROB)[8](t()[1][7][5][.][5][)][EXE]
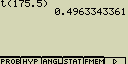
[F1](PROB)[5](P()[0][.][4][9][6][-]
[F1](PROB)[5](P()[(-)][1][.][6][3][4][)][EXE]
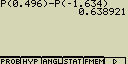 (63.9% z celku má výšku v zadaném rozmezí)
(63.9% z celku má výšku v zadaném rozmezí)
[F1](PROB)[7](R()[0][.][4][9][6][)][EXE]
 (31.0% je vyšší než zadaná hodnota)
(31.0% je vyšší než zadaná hodnota)
Graf rozdělení pravděpodobnosti
V módu RUN.MAT je možné spočítat a vynést
graf rozdělení pravděpodobnosti
- Vstup do módu RUN.MAT
- Zadej příkazy pro nakreslení grafu v pravoúhlých souřadnicích
- Zadej hodnotu pravděpodobnosti
Nakresli graf rozdělení pravděpodobnosti pro P(0.5)
Postup:
- Vstup do módu RUN.MAT
- [OPTN][F6](
 )[F6](
)[F6]( )[F2](SKTCH)[1](Cls)[EXE]
)[F2](SKTCH)[1](Cls)[EXE]

[F2](SKTCH)[4](GRPH)[1](Y=)
[OPTN][F6]( )[F1](PROB)[5](P()[0][.][5]
)[F1](PROB)[5](P()[0][.][5]
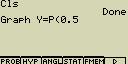
-
[EXE]