| Solve
(CAS, ALGEBRA) |
| Popis funkce |
| vyřeší rovnici nebo vyjádří proměnnou |
| Zadání |
CAS, TUTOR: [F1](TRNS)[4](solve)
ALGEBRA: [F1](TRNS)[5](solve) |
| Syntaxe |
solve( výraz , proměnná
)
solve( rovnice , proměnná )
solve( nerovnice , proměnná )
* pokud není proměnná zadána, je za ní považováno
X
řešení více lineárních rovnic:
solve( { rovnice 1 ,
rovnice 2 , ... , rovnice n } ,
{ proměnná 1 , proměnná 2 , ... , proměnná
n }
)
*proměnných musí být stejně jako rovnic |
| Příklad |
| 1. |
|
Vyřeš rovnici AX2+BX-C=0
[F1](TRNS)[4](solve)[ALPHA]
[A][X^2][+][ALPHA][B][-]
[ALPHA][C][SHIFT][=][0][EXE]
|
 |
| 2. |
|
solve( A+B = C, A ) |
{ A = -B+C } |
| 3. |
|
solve((X2-2)/(X-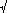 2)=0,X) 2)=0,X) |
{X = -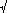 2} 2} |
| 4. |
|
solve( 3X+2Y-11 = 0, Y ) |
{ Y= -3X/2 + 11/2 } |
| 5. |
|
solve( 1/(X-7) = 1/(3X+8), X ) |
{ X = -15/2 } |
| 6. |
|
solve( (X2-1)/(X2+1)+1 = 0, X ) |
{ X = 0 } |
| 7. |
|
solve( 2X-1 < 3, X ) |
{ X < 2 } |
| 8. |
|
solve( 1/X 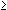 0, X ) 0, X ) |
{ 0 < x} |
| 9. |
|
solve( X/((X-1)(X+1)) 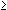 0, X )
0, X ) |
{ -1 < X 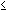 0, 1 < x} 0, 1 < x} |
| 10. |
|
solve( Abs(2X-1) < 3, X ) |
{ -1 < X < 2 } |
| 11. |
|
solve( (X2+4X)/(X+3) < 3, X ) |
{ X < -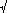 (37)/2 - 1/2, (37)/2 - 1/2,
-3 < X < 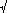 (37)/2 - 1/2 } (37)/2 - 1/2 } |
| 12. |
|
solve( X2+X-1 = 0, X ) |
{ X = (-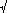 (5))/2 - 1/2, (5))/2 - 1/2,
X = 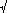 (5)/2 - 1/2 } (5)/2 - 1/2 } |
| 13. |
|
solve( 4X2+2X-4 = X2+2X, X ) |
{X = -2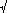 (3)/3, (3)/3,
X = 2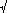 (3)/3 } (3)/3 } |
| 14. |
|
solve( X4 + 1 = 0, X ) |
No solution
<reálná čísla> |
| 15. |
|
solve( X2 - Abs(X) - 2 = 0, X ) |
{ X = -2, X = 2 } |
| 16. |
|
solve( 2X + Abs(X-2) = 6, X ) |
{ X = 8/3 } |
| 17. |
|
solve( Abs(X-1) + (X+3) = 5, X |
{ X = 3/2 } |
| 18. |
|
solve( Abs(X-1) + Abs(X+3) = 5, X ) |
{ X = -7/2, X = 3/2 } |
| 19. |
|
solve( (X2-2)/(X-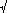 (2)) = 0, X ) (2)) = 0, X ) |
{ X = -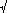 2 } 2 } |
| 20. |
|
solve( 2^X = 3^X, X ) |
{ X = 0 } |
| 21. |
|
solve( 9^X + 3^X = 2, X ) |
{ X = 0 }
<reálná čísla> |
| 22. |
|
solve( Abs(2X-1) = 3, X ) |
{ X = -1, X = 2 } |
| 23. |
|
solve( ln(X2-4X+3) = ln(3), X ) |
{ X = 0, X = 4 } |
| 24. |
|
solve( ln(X2-1) + ln(X2-X) = ln(X), X ) |
{ X = (-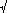 (5))/2 + 1/2, (5))/2 + 1/2,
X = (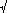 (5))/2 + 1/2 } (5))/2 + 1/2 } |
| 25. |
|
solve( ln(X+2) + 1=ln(X-1) + ln(2), X ) |
{ X = -2/e-2 - 2e/e-2 } |
| 26. |
|
solve( ln(2^X) = ln(3^X), X ) |
{ X = 0 } |
| 27. |
|
solve( sin(X), X ) |
{ X = 2pk, X = 2pk +
p} |
| 28. |
|
solve( X sin(X)+sin(X), X ) |
{ X = -1, X = 2pk,
X = 2pk + p} |
| 29. |
|
solve( 2 cos(X) + 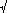 3 = 0, X ) 3 = 0, X ) |
{ X = 2pk - 5p/6,
X = -2pk + 5p/6 } |
| 30. |
|
solve( 4 cos(X)2 - 1 = 0, X ) |
{ X = 2pk - 2p/3,
X = 2pk - p/3,
X = -2pk + p/3,
X = -2pk + 2p/3 } |
| 31. |
|
solve( 2 sin(X)2 +
cos(X)2 - 3/2=0, X ) |
{ X = 2pk - 3p/4,
X = 2pk - p/4,
X = 2pk + p/4,
X = 2pk + 3p/4 } |
| 32. |
|
solve( -ABX2+AX^3+X2-3BX+2X2 ) |
{ X = 0, X = -3/A, X = B } |
| 33. |
|
solve( -4X2-4 ) |
No solution
<reálná čísla>
{ X = -i, X = i }
<komplexní čísla> |
| 34. |
|
solve( eX - e(-X) = 8/3, X ) |
{ X = ln(3) }
<reálná čísla>
{ X = ln(3), X= pi - ln(3) }
<komplexní čísla> |
| 35. |
|
solve( e(2X+1) + 3e(X+1) = 4e1 |
{ X = 0 }
<reálná čísla>
{ X = 0, X = pi + 2 ln(2) }
<komplexní čísla> |
|
soustava lineárních
rovnic |
| 36. |
|
solve( {X+AY=3, XB+4=6}, {X, Y} ) |
{ X=2/B, Y=(3B-2)/AB } |
| 37. |
|
solve( {10X-4Y=0, 8+10X-5Y=0}, {X, Y} ) |
{ X=16/5, Y=8 } |
| 38. |
|
solve( {6+6H+2S=0, -4H-4S=0}, {H, S} ) |
{ H= -3/2, S=3/2 } |
| 39. |
|
solve( {-2+7X+8A=0, 5+9A-5W=0, -3+X+3W=0}, {X, A, W} ) |
{ X=54/149, A= -10/149, W=131/149 } |
|
|
|
| Substituce
(CAS, ALGEBRA, TUTOR) |
| Popis funkce |
| dosadí do výrazu za proměnnou |
| Zadání |
CAS: [F1](TRNS)[9](sbstit)
ALGEBRA: [F1](TRNS)[8](sbstit)
TUTOR: [F1](TRNS)[7](sbstit) |
| Syntaxe |
substitute( výraz , proměnná = výraz , proměnná = výraz
, ...)
substitute( rovnice , proměnná = výraz , proměnná = výraz
, ... )
substitute( nerovnice , proměnná = výraz
, proměnná = výraz , ... ) |
| Příklad |
| 1. |
|
do rovnice 2X-1 dosaď hodnotu X=5
|
|
|
CAS: |
|
|
|
[F1](TRNS)[9](sbstit)
[2][X][-][1][,][X][=][5][EXE] |
 |
|
ALGEBRA: |
|
|
|
[F1](TRNS)[8](sbstit)
[2][X][-][1][,][X][=][5][EXE] |
 |
| 2. |
|
substitute( 2X+1, X = 5 ) |
11 (CAS)
5
 2 + 1 (ALGEBRA)
2 + 1 (ALGEBRA) |
| 3. |
|
substitute( 3X+5Y, X = 3, Y = 7 ) |
384 (CAS)
3  3 + 7
3 + 7  5 (ALGEBRA)
5 (ALGEBRA) |
| 4. |
|
substitute( 2X+3Y=5, Y=3X+1 ) |
2X+3(3X+1) = 5 |
| 5. |
|
substitute(3X+5Y-Z=9, Y=2X, Z=2X-3) |
11X+3 = 9 |
| 6. |
|
substitute(A+2B+3C+4D > 0, A =
2+D, B = 2D-1, C = D2 ) |
3D2+9D > 0 |
|
|
|




